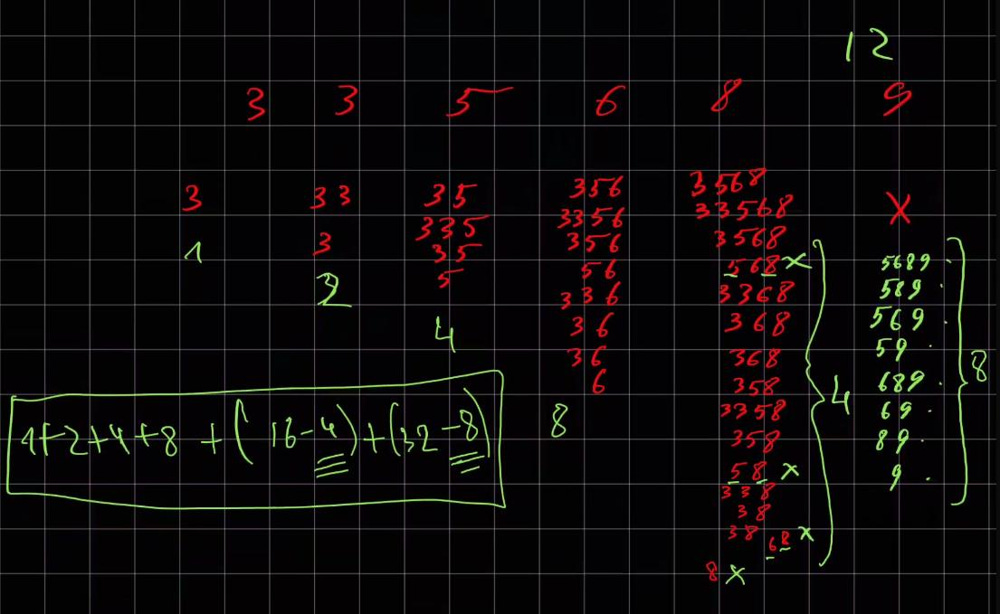Leetcode daily # 6.05.2023

[1498. Number of Subsequences That Satisfy the Given Sum Condition]

6.05.2023

1498. Number of Subsequences That Satisfy the Given Sum Condition medium

fun numSubseq(nums: IntArray, target: Int): Int {
    val m = 1_000_000_007
    nums.sort()
    val cache = IntArray(nums.size + 1) { 0 }
    cache[1] = 1
    for (i in 2..nums.size) cache[i] = (2 * cache[i - 1]) % m
    var total = 0
    nums.forEachIndexed { i, n ->
        var lo = 0
        var hi = i
        var removed = cache[i + 1]
        while (lo <= hi) {
            val mid = lo + (hi - lo) / 2
            if (nums[mid] + n <= target) {
                removed = cache[i - mid]
                lo = mid + 1
            } else hi = mid - 1
        }
        total = (total + cache[i + 1] - removed) % m
    }
    if (total < 0) total += m
    return total
}

blog post

Join me on Telegram

https://t.me/leetcode_daily_unstoppable/204

Intuition

1. We can safely sort an array, because order doesn’t matter for finding max or min in a subsequence.

2. Having increasing order gives us the pattern:
   

1. Ignoring the target, each new number adds the previous value to the sum: sum2=sum1+(1+sum1)sum2​=sum1​+(1+sum1​), or just 2i2i.

2. Let’s observe the pattern of the removed items:
   

1. For example, target = 12, for number 8, count of excluded values is 4 = [568, 58, 68, 8]; for number 9, it is 8 = [5689, 589, 569, 59, 689, 69, 89, 9]. We can observe, it is determined by the sequence 5 6 8 9, where all the numbers are bigger, than target - 9. That is, the law for excluding the elements is the same: r2=r1+(1+r1)r2​=r1​+(1+r1​), or just 2x2x, where x - is the count of the bigger numbers.

Approach

• Precompute the 2-powers

• Use binary search to count how many numbers are out of the equation n_i + x <= target

• A negative result can be converted to positive by adding the modulo 1_000_000_7

Complexity

• Time complexity:
  O(nlog(n))

• Space complexity:
  O(n)