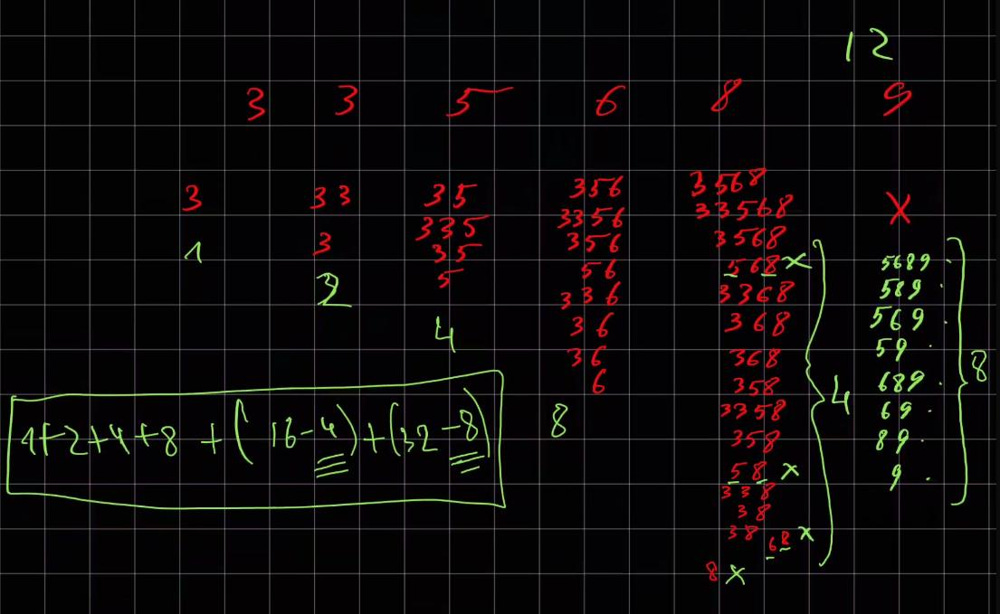Leetcode daily # 6.05.2023
[1498. Number of Subsequences That Satisfy the Given Sum Condition]
6.05.2023
1498. Number of Subsequences That Satisfy the Given Sum Condition medium
fun numSubseq(nums: IntArray, target: Int): Int {
val m = 1_000_000_007
nums.sort()
val cache = IntArray(nums.size + 1) { 0 }
cache[1] = 1
for (i in 2..nums.size) cache[i] = (2 * cache[i - 1]) % m
var total = 0
nums.forEachIndexed { i, n ->
var lo = 0
var hi = i
var removed = cache[i + 1]
while (lo <= hi) {
val mid = lo + (hi - lo) / 2
if (nums[mid] + n <= target) {
removed = cache[i - mid]
lo = mid + 1
} else hi = mid - 1
}
total = (total + cache[i + 1] - removed) % m
}
if (total < 0) total += m
return total
}
Join me on Telegram
https://t.me/leetcode_daily_unstoppable/204
Intuition
We can safely sort an array, because order doesn’t matter for finding
maxorminin a subsequence.Having increasing order gives us the pattern:
Ignoring the
target, each new number adds the previous value to the sum: sum2=sum1+(1+sum1)sum2=sum1+(1+sum1), or just 2i2i.Let’s observe the pattern of the removed items:
For example,
target = 12, for number8, count of excluded values is4= [568, 58, 68, 8]; for number9, it is8= [5689, 589, 569, 59, 689, 69, 89, 9]. We can observe, it is determined by the sequence5 6 8 9, where all the numbers are bigger, thantarget - 9. That is, the law for excluding the elements is the same: r2=r1+(1+r1)r2=r1+(1+r1), or just 2x2x, where x - is the count of the bigger numbers.
Approach
Precompute the 2-powers
Use binary search to count how many numbers are out of the equation
n_i + x <= targetA negative result can be converted to positive by adding the modulo
1_000_000_7
Complexity
Time complexity:
O(nlog(n))Space complexity:
O(n)