Max top k valued intervals #hard #binary_search #dp
Intuition
Used a hint: dp + binary search for the next item. The interesting part is bottom up dp:
for every interval look up the largest previous result before start
append if prev + value > curr
the dp row is increased pairs end, sum
meaning max value at the end time
the longest chain of events is k
Approach
sort by start or end, both works
Complexity
Time complexity: $$O(nklog(n))$$
Space complexity: $$O(nk)$$
Code
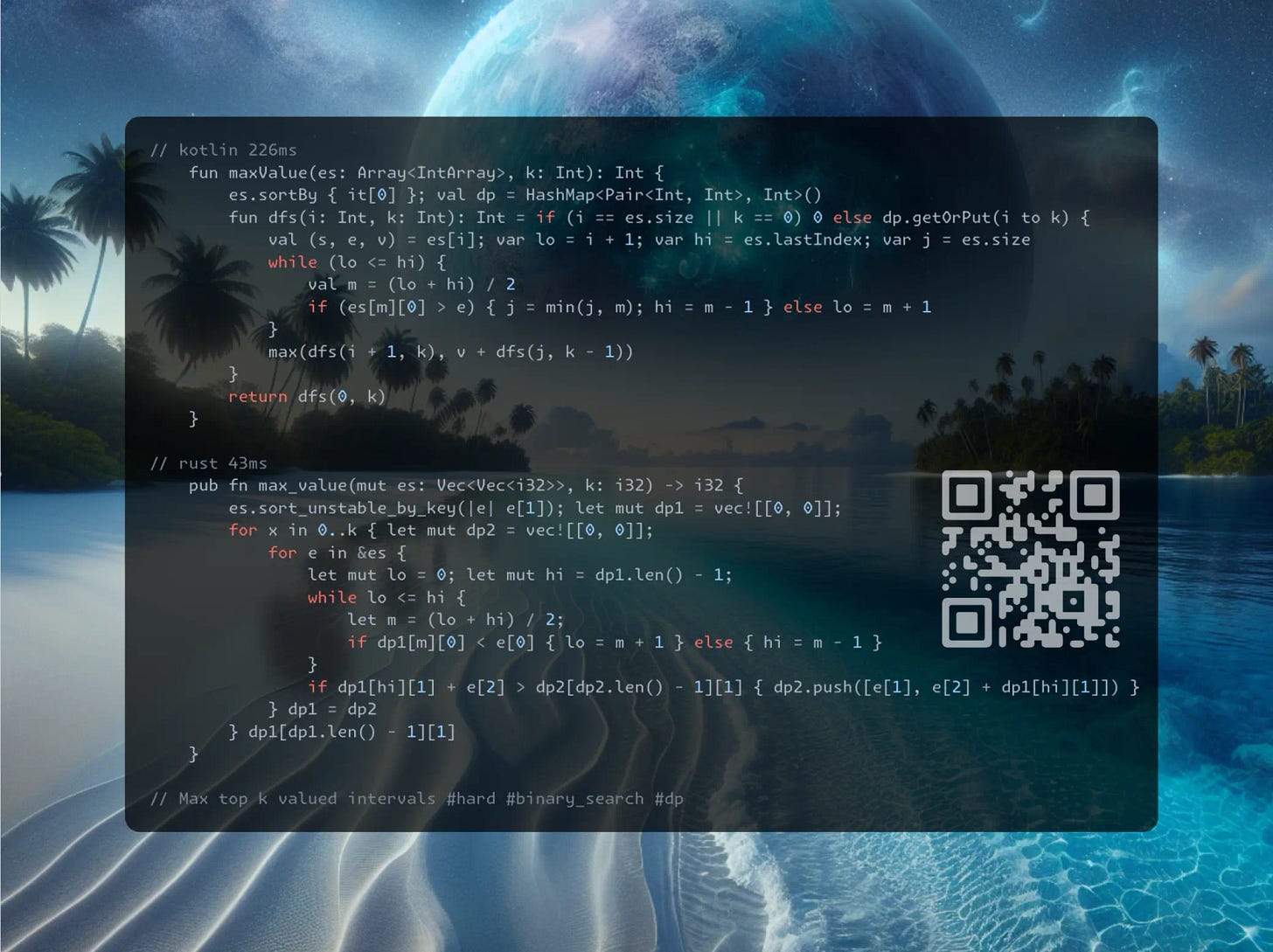
// 226ms
fun maxValue(es: Array<IntArray>, k: Int): Int {
es.sortBy { it[0] }; val dp = HashMap<Pair<Int, Int>, Int>()
fun dfs(i: Int, k: Int): Int = if (i == es.size || k == 0) 0 else dp.getOrPut(i to k) {
val (s, e, v) = es[i]; var lo = i + 1; var hi = es.lastIndex; var j = es.size
while (lo <= hi) {
val m = (lo + hi) / 2
if (es[m][0] > e) { j = min(j, m); hi = m - 1 } else lo = m + 1
}
max(dfs(i + 1, k), v + dfs(j, k - 1))
}
return dfs(0, k)
}
// 208ms
fun maxValue(es: Array<IntArray>, k: Int): Int {
es.sortBy { it[1] }
var dp1 = arrayListOf(listOf(0, 0))
var dp2 = arrayListOf(listOf(0, 0))
repeat(k) {
for ((s, e, v) in es) {
var lo = 0; var hi = dp1.size - 1; var i = -1
while (lo <= hi) {
val m = (lo + hi) / 2
if (dp1[m][0] < s) { lo = m + 1; i = max(i, m) } else { hi = m - 1 }
}
if (i >= 0 && dp1[i][1] + v > dp2.last()[1]) dp2 += listOf(e, dp1[i][1] + v)
}
dp1 = dp2; dp2 = arrayListOf(listOf(0, 0))
}
return dp1.last()[1]
}
// 43ms
pub fn max_value(mut es: Vec<Vec<i32>>, k: i32) -> i32 {
es.sort_unstable_by_key(|e| e[1]); let mut dp1 = vec![[0, 0]];
for x in 0..k { let mut dp2 = vec![[0, 0]];
for e in &es {
let mut lo = 0; let mut hi = dp1.len() - 1;
while lo <= hi {
let m = (lo + hi) / 2;
if dp1[m][0] < e[0] { lo = m + 1 } else { hi = m - 1 }
}
if dp1[hi][1] + e[2] > dp2[dp2.len() - 1][1] { dp2.push([e[1], e[2] + dp1[hi][1]]) }
} dp1 = dp2
} dp1[dp1.len() - 1][1]
}
// 502ms
int maxValue(vector<vector<int>>& es, int k) {
sort(es.begin(), es.end()); unordered_map<long long, int> dp;
auto dfs = [&](this const auto& dfs, int i, int k) -> int {
if (i == es.size() || k == 0) return 0;
long long key = ((long long)i << 32) | k;
if (dp.count(key)) return dp[key];
int s = es[i][0], e = es[i][1], v = es[i][2],
lo = i + 1, hi = es.size() - 1;
while (lo <= hi) {
int m = (lo + hi) / 2;
if (es[m][0] > e) hi = m - 1; else lo = m + 1;
}
return dp[key] = max(dfs(i + 1, k), v + dfs(lo, k - 1));
};
return dfs(0, k);
}
