# 25.06.2025 [2040. Kth Smallest Product of Two Sorted Arrays]

K-th increasing product from two arrays #hard #binary_search

25.06.2025

2040. Kth Smallest Product of Two Sorted Arrays hard blog post substack youtube

Join me on Telegram

https://t.me/leetcode_daily_unstoppable/1030

Problem TLDR

K-th increasing product from two arrays #hard #binary_search

Intuition

The intuition is simple (i used the hints though):

• search result with binary search

• count by iterating over one array and finding how many to take using the binary search in the other.

The implementation is scary.

    // 1 2 3       1x1 1x2 2x1 1x3 3x1 2x2 2x3 3x2 3x3
    // 1 2 3

    // 2 5    2x3 2x4 5x3 5x4 
    // 3 4      6   8  15  20

    // ----++++    ----+++
    //               
    // inverted for ----- + classic for +++++   

Approach

• we only need one classic binary search and one inverted

• for the negative current array use the inverted search; divide array into negative and positive part

• search for the maximum index you can take

• for inverted, subtract inverted result from all possible pairs

Complexity

• Time complexity: $$O(nlog^2(n))$$

• Space complexity: $$O(1)$$

Code

// 1022ms
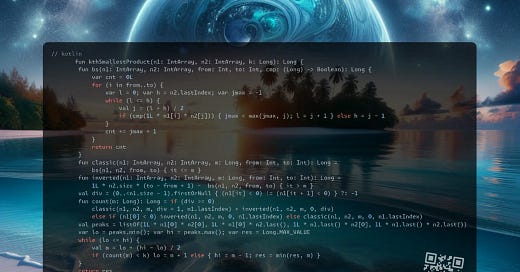
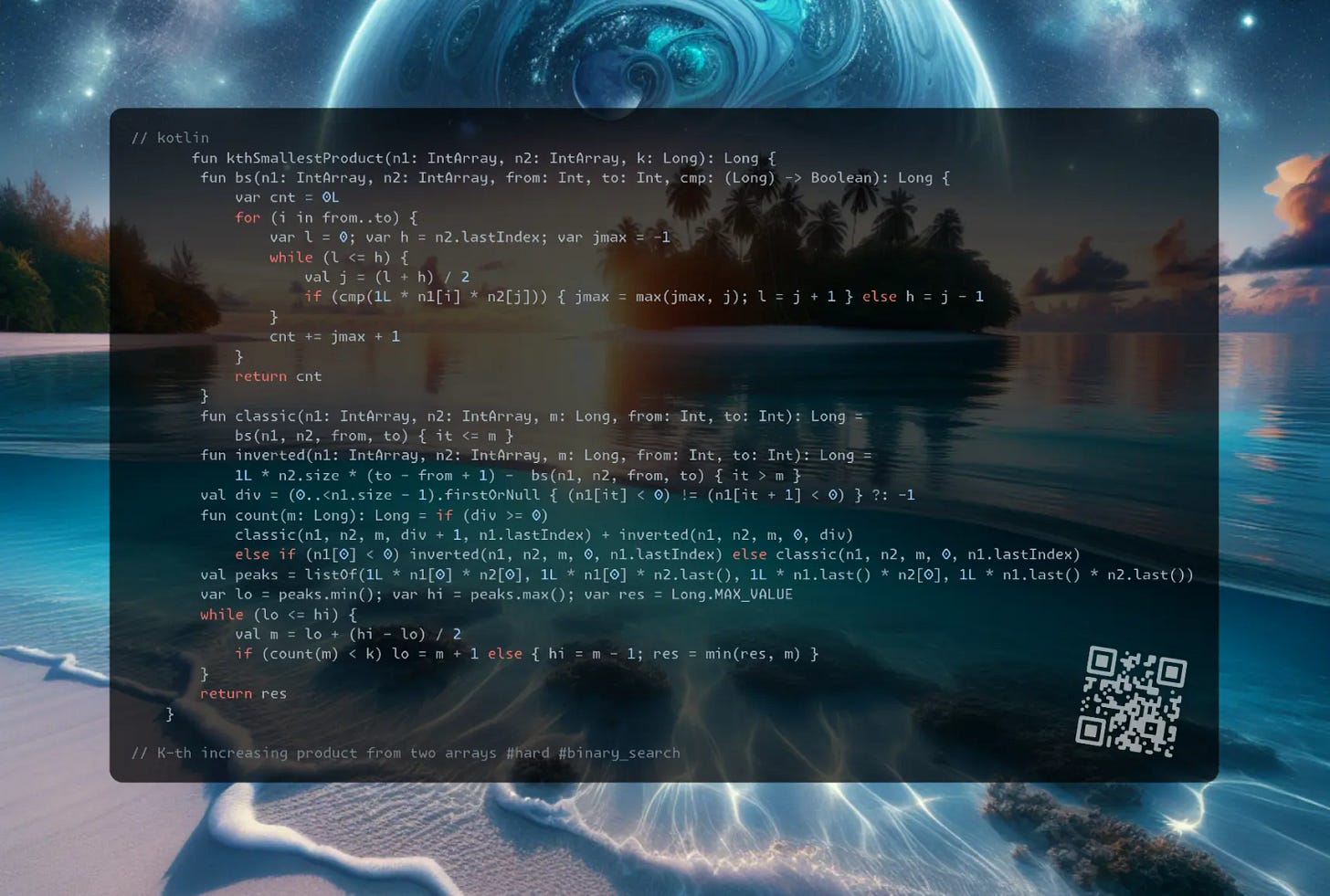
    fun kthSmallestProduct(n1: IntArray, n2: IntArray, k: Long): Long {
        fun bs(n1: IntArray, n2: IntArray, from: Int, to: Int, cmp: (Long) -> Boolean): Long {
            var cnt = 0L
            for (i in from..to) {
                var l = 0; var h = n2.lastIndex; var jmax = -1
                while (l <= h) {
                    val j = (l + h) / 2
                    if (cmp(1L * n1[i] * n2[j])) { jmax = max(jmax, j); l = j + 1 } else h = j - 1
                }
                cnt += jmax + 1
            }
            return cnt
        }
        fun classic(n1: IntArray, n2: IntArray, m: Long, from: Int, to: Int): Long =
            bs(n1, n2, from, to) { it <= m }
        fun inverted(n1: IntArray, n2: IntArray, m: Long, from: Int, to: Int): Long =
            1L * n2.size * (to - from + 1) -  bs(n1, n2, from, to) { it > m }
        val div = (0..<n1.size - 1).firstOrNull { (n1[it] < 0) != (n1[it + 1] < 0) } ?: -1
        fun count(m: Long): Long = if (div >= 0)
            classic(n1, n2, m, div + 1, n1.lastIndex) + inverted(n1, n2, m, 0, div)
            else if (n1[0] < 0) inverted(n1, n2, m, 0, n1.lastIndex) else classic(n1, n2, m, 0, n1.lastIndex)
        val peaks = listOf(1L * n1[0] * n2[0], 1L * n1[0] * n2.last(), 1L * n1.last() * n2[0], 1L * n1.last() * n2.last())
        var lo = peaks.min(); var hi = peaks.max(); var res = Long.MAX_VALUE
        while (lo <= hi) {
            val m = lo + (hi - lo) / 2
            if (count(m) < k) lo = m + 1 else { hi = m - 1; res = min(res, m) }
        }
        return res
    }