# 22.07.2023 [688. Knight Probability in Chessboard]

Probability of making `k` steps on a chessboard without stepping outside

22.07.2023

688. Knight Probability in Chessboard medium
blog post

Join me on Telegram

https://t.me/leetcode_daily_unstoppable/283

Problem TLDR

Probability of making k steps on a chessboard without stepping outside

Intuition

The description example doesn’t give a clear picture of how the probability works.

• individual probability is 1/8 each time we make a step.

• One step is 1/8, two steps are 1/8 * 1/8 and so on.

• So, the k-steps path will have probability of 1/8^k

• we need to sum all the probabilities of individual k-steps paths, that will remain on a board

• the brute force algorithm for this will be BFS:

• for k rounds:

• poll all the elements, and make possible steps on the board

• resulting probability will be queue.size / 8^k, as queue will contain only the final possible ways after k steps

However, there are too many possible ways, we will quickly run out of memory.

It is noticeable, some ways are repeating, and after s steps the same cell [x, y] produces the same amount of possible ways dp[x, y][s]. We can cache this result for each cell.

However, the number of ways are still very big and do not fit into Long 64 bits. To solve this, we can cache not only the ways, but the probability, dividing each step by 8.

Approach

• storing the directions in a sequence helps to reduce some LOC

Complexity

• Time complexity:
  O(kn^2)

• Space complexity:
  O(kn^2)

Code

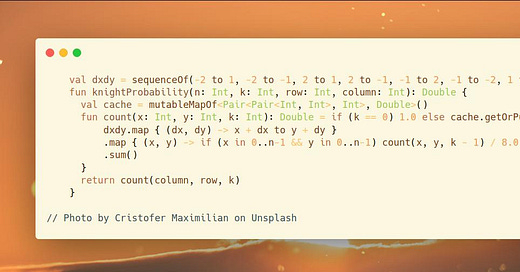
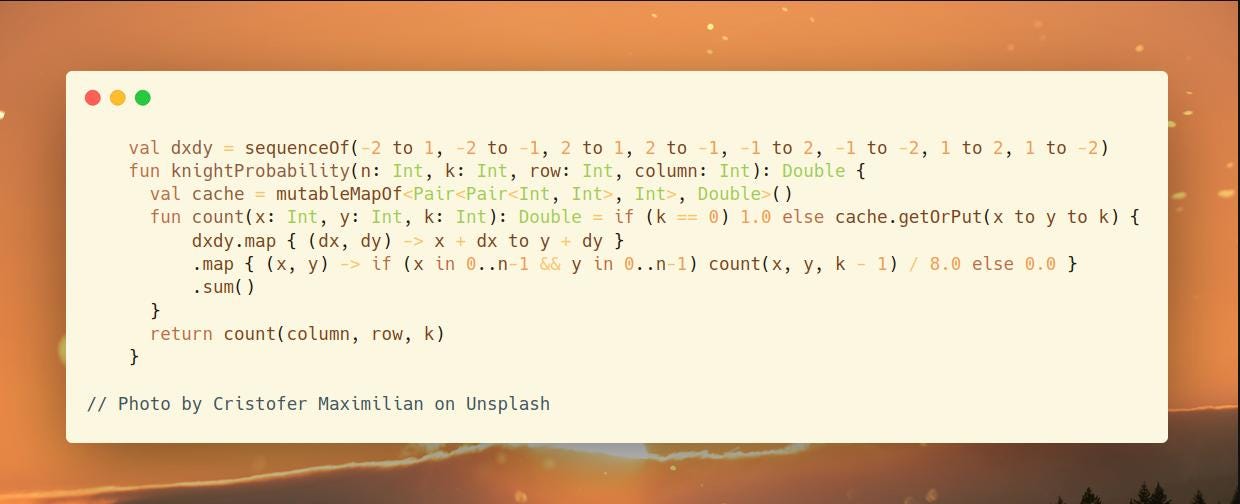
    val dxdy = sequenceOf(-2 to 1, -2 to -1, 2 to 1, 2 to -1, -1 to 2, -1 to -2, 1 to 2, 1 to -2)
    fun knightProbability(n: Int, k: Int, row: Int, column: Int): Double {
      val cache = mutableMapOf<Pair<Pair<Int, Int>, Int>, Double>()
      fun count(x: Int, y: Int, k: Int): Double = if (k == 0) 1.0 else cache.getOrPut(x to y to k) {
          dxdy.map { (dx, dy) -> x + dx to y + dy }
          .map { (x, y) -> if (x in 0..n-1 && y in 0..n-1) count(x, y, k - 1) / 8.0 else 0.0 }
          .sum()
      }
      return count(column, row, k)
    }

The magical rundown

Step ₀ - The High Noon Duel 🤠🎵🌵:
🎶 The town clock strikes twelve, and the high noon chess duel commences. A 
lone knight 🐎 trots onto the scorching, sun-bleached chessboard, casting a long 
shadow on the sandy squares.

╔═══🌵═══🌵═══╗
║ 🐎 ║   ║    ║
╠═══🌵═══🌵═══╣
║   ║    ║   ║
╠═══🌵═══🌵═══╣
║   ║    ║   ║
╚═══🌵═══🌵═══╝

The Sheriff 🤠, ever the statistician, watches keenly. "For now, the odds are 
all in your favor, Knight," he says, unveiling the initial probability 𝓹₀ = 1.
┌─────💰────┬────💰────┬────💰────┐
│     1     │    0    │     0    │
├─────💰────┼────💰────┼────💰────┤
│     0     │    0    │     0    │
├─────💰────┼────💰────┼────💰────┤
│     0     │    0    │     0    │
└─────💰────┴────💰────┴────💰────┘

Step ₁ - The Dusty Trail 🌄🎵🐴:
🎶 The knight 🐎 leaps into action, stirring up a cloud of dust. He lands in two 
different squares, each with a calculated 1/8 chance. The Sheriff 🤠 nods 
approvingly. "Bold moves, Knight. The probability after this is 𝓹₁ = 1/8 + 1/8 = 1/4."
╔═══🌵═══🌵═══╗
║   ║    ║   ║
╠═══🌵═══🌵═══╣
║   ║    ║ 🐎 ║
╠═══🌵═══🌵═══╣
║   ║ 🐎 ║   ║
╚═══🌵═══🌵═══╝

He reveals the new odds:
┌─────💰────┬────💰────┬────💰────┐
│     0     │    0    │     0    │
├─────💰────┼────💰────┼────💰────┤
│     0     │    0    │    ¹/₈   │
├─────💰────┼────💰────┼────💰────┤
│     0     │   ¹/₈   │     0    │
└─────💰────┴────💰────┴────💰────┘

Step ₂ - The Sun-Baked Crossroads ☀️🎵🌪️:
🎶 The knight 🐎 continues his daring maneuvers, hopping onto a few critical 
spots. He lands on three squares, with probabilities of 1/64, 1/64, and 2/64. 
Adding these up, the Sheriff 🤠 declares, "The stakes have risen, Knight. The 
total is 𝓹₂ = 1/64 + 1/64 + 2/64 = 1/16."
╔═══🌵═══🌵═══╗
║🐎🐎║   ║ 🐎 ║
╠═══🌵═══🌵═══╣
║   ║    ║   ║
╠═══🌵═══🌵═══╣
║ 🐎 ║   ║   ║
╚═══🌵═══🌵═══╝

The updated odds take shape:
┌─────💰────┬────💰────┬────💰────┐
│    ²/₆₄   │    0    │   ¹/₆₄   │
├─────💰────┼────💰────┼────💰────┤
│     0     │    0    │     0    │
├─────💰────┼────💰────┼────💰────┤
│    ¹/₆₄   │    0    │     0    │
└─────💰────┴────💰────┴────💰────┘

Step ₃ - The Outlaw's Hideout 🏚️🎵🐍:
🎶 As the sun sets, the knight 🐎 lands in a few hidden spots with various 
probabilities. Each calculated leap adds to his total: 1/512 + 1/512 + 3/512 + 3/512. 
The Sheriff 🤠 raises an eyebrow. "Well played, Knight. Your total now is 𝓹₃ = 
1/512 + 1/512 + 3/512 + 3/512."

╔═══🌵═══🌵═══╗
║   ║ 🐎 ║    ║
╠═══🌵═══🌵═══╣
║ 🐎 ║   ║🐎🐎🐎║
╠═══🌵═══🌵═══╣
║   ║🐎🐎🐎║  ║
╚═══🌵═══🌵═══╝

Beneath the twinkling stars, the Sheriff 🤠 surveys the evolving game. "You're 
not an easy one to beat, Knight," he admits, revealing the updated stakes:
┌─────💰────┬────💰────┬────💰────┐
│     0     │  ¹/₅₁₂  │     0    │
├─────💰────┼────💰────┼────💰────┤
│   ¹/₅₁₂   │    0    │   ³/₅₁₂  │
├─────💰────┼────💰────┼────💰────┤
│     0     │  ³/₅₁₂  │     0    │
└─────💰────┴────💰────┴────💰────┘

🎶 So, under the twinkling stars and to the tune of the whistling wind, our 
knight's adventure continues into the night. The stakes are high, the moves 
unpredictable, but one thing's certain: this wild chess duel is far from over! 🌵🐎🌌🎵