# 21.06.2023 [2448. Minimum Cost to Make Array Equal]

Min cost to make all `arr[i]` equal, where each change is `cost[i]`

21.06.2023

2448. Minimum Cost to Make Array Equal hard
blog post

Join me on Telegram

https://t.me/leetcode_daily_unstoppable/252

Problem TLDR

Min cost to make all arr[i] equal, where each change is cost[i]

Intuition

First idea is that at least one element can be unchanged.
Assume, that we want to keep the most costly element unchanged, but this will break on example:

1 2 2 2    2 1 1 1
f(1) = 0 + 1 + 1 + 1 = 3
f(2) = 2 + 0 + 0 + 0 = 2 <-- more optimal

Let’s observe the resulting cost for each number:

//    1 2 3 2 1     2 1 1 1 1
//0:  2 2 3 2 1 = 10
//1:  0 1 2 1 0 = 4
//2:  2 0 1 0 1 = 4
//3:  4 1 0 1 2 = 8
//4:  6 2 1 2 3 = 14

We can see that f(x) have a minimum and is continuous. We can find it with Binary Search, comparing the slope = f(mid + 1) - f(mid - 1). If slope > 0, minimum is on the left.

Approach

For more robust Binary Search:

• use inclusive lo, hi

• always compute the result min

• always move the borders lo = mid + 1 or hi = mid - 1

• check the last case lo == hi

Complexity

• Time complexity:
  O(nlog(n))

• Space complexity:
  O(1)

Code

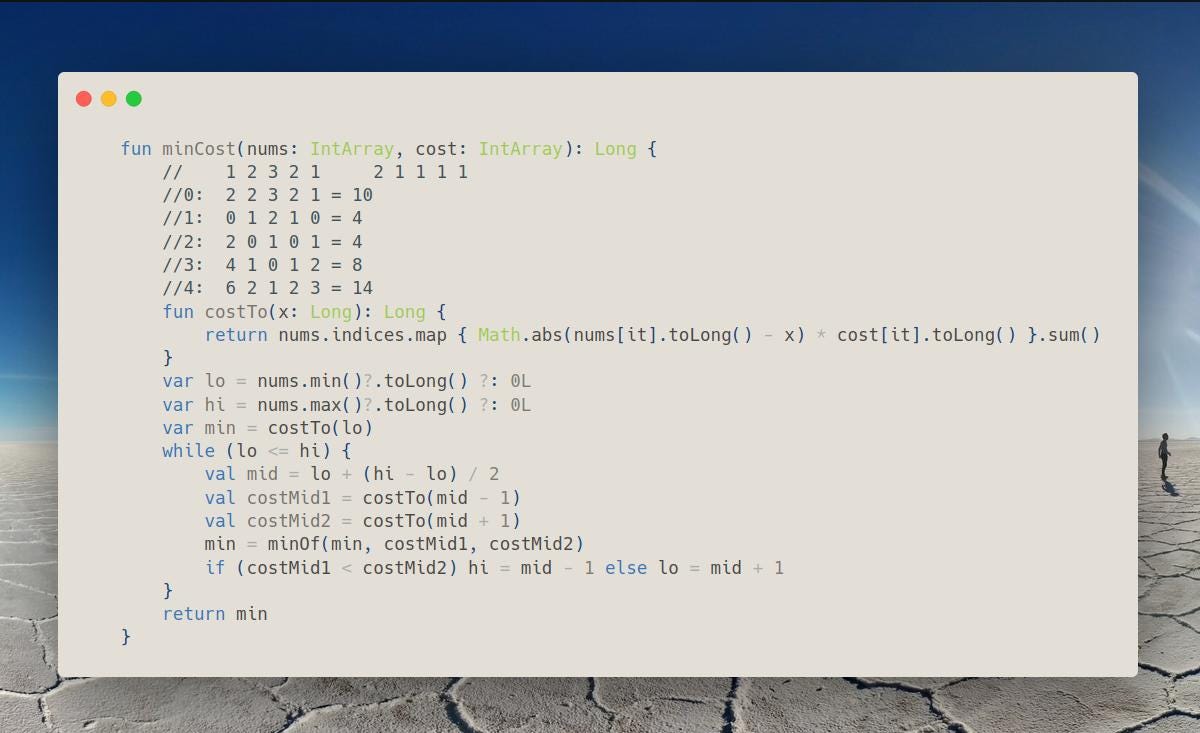
fun minCost(nums: IntArray, cost: IntArray): Long {
    //    1 2 3 2 1     2 1 1 1 1
    //0:  2 2 3 2 1 = 10
    //1:  0 1 2 1 0 = 4
    //2:  2 0 1 0 1 = 4
    //3:  4 1 0 1 2 = 8
    //4:  6 2 1 2 3 = 14
    fun costTo(x: Long): Long {
        return nums.indices.map { Math.abs(nums[it].toLong() - x) * cost[it].toLong() }.sum()
    }
    var lo = nums.min()?.toLong() ?: 0L
    var hi = nums.max()?.toLong() ?: 0L
    var min = costTo(lo)
    while (lo <= hi) {
        val mid = lo + (hi - lo) / 2
        val costMid1 = costTo(mid - 1)
        val costMid2 = costTo(mid + 1)
        min = minOf(min, costMid1, costMid2)
        if (costMid1 < costMid2) hi = mid - 1 else lo = mid + 1
    }
    return min
}