# 21.01.2025 [2017. Grid Game]

Maximum of minimized paths #medium #prefix_sum

21.01.2025

2017. Grid Game medium blog post substack youtube

Join me on Telegram

https://t.me/leetcode_daily_unstoppable/871

Problem TLDR

Maximum of minimized paths #medium #prefix_sum

Intuition

Observe some examples:

    // 0  1  2  3  4  5  6  7  8  9
    // 0 ,3 ,20,17,2 ,12,15,17,4 ,15
    // 20,10,13,14,15,5 ,2 ,3 ,14,3

    // 0  1  2  3  4  5  6  7  8  9
    //                12,15,17,4 ,15
    // 20,10,13,14


    // 0 1 2
    // 2 5 4
    // 1 5 1
    // *      a = 5+4=9 b = 0
    //   *

The optimal strategy of the minimizer is not to maximize it's own path.

The second robot path is either bottom left or top right prefix sums. Choose the minimium between any possible splits of them.

Approach

• to find this insight you have to draw what possible paths can the second robot take

• minimize the maximum of a and b: first robot minimizes, second maximizes

Complexity

• Time complexity: O(n)

• Space complexity: O(1)

Code

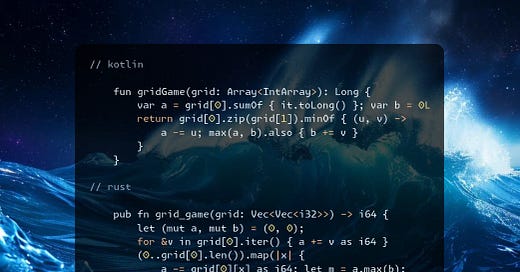
    fun gridGame(grid: Array<IntArray>): Long {
        var a = grid[0].sumOf { it.toLong() }; var b = 0L
        return grid[0].zip(grid[1]).minOf { (u, v) ->
            a -= u; max(a, b).also { b += v }
        }
    }

    pub fn grid_game(grid: Vec<Vec<i32>>) -> i64 {
        let (mut a, mut b) = (0, 0); 
        for &v in grid[0].iter() { a += v as i64 }
        (0..grid[0].len()).map(|x| {
            a -= grid[0][x] as i64; let m = a.max(b);
            b += grid[1][x] as i64; m
        }).min().unwrap()
    }

    long long gridGame(vector<vector<int>>& g) {
        long long a = 0, b = 0, r = 1e18; for (int v: g[0]) a += v;
        for (int x = 0; auto v: g[0])
            a -= v, r = min(r, max(a, b)), b += g[1][x++];
        return r;
    }