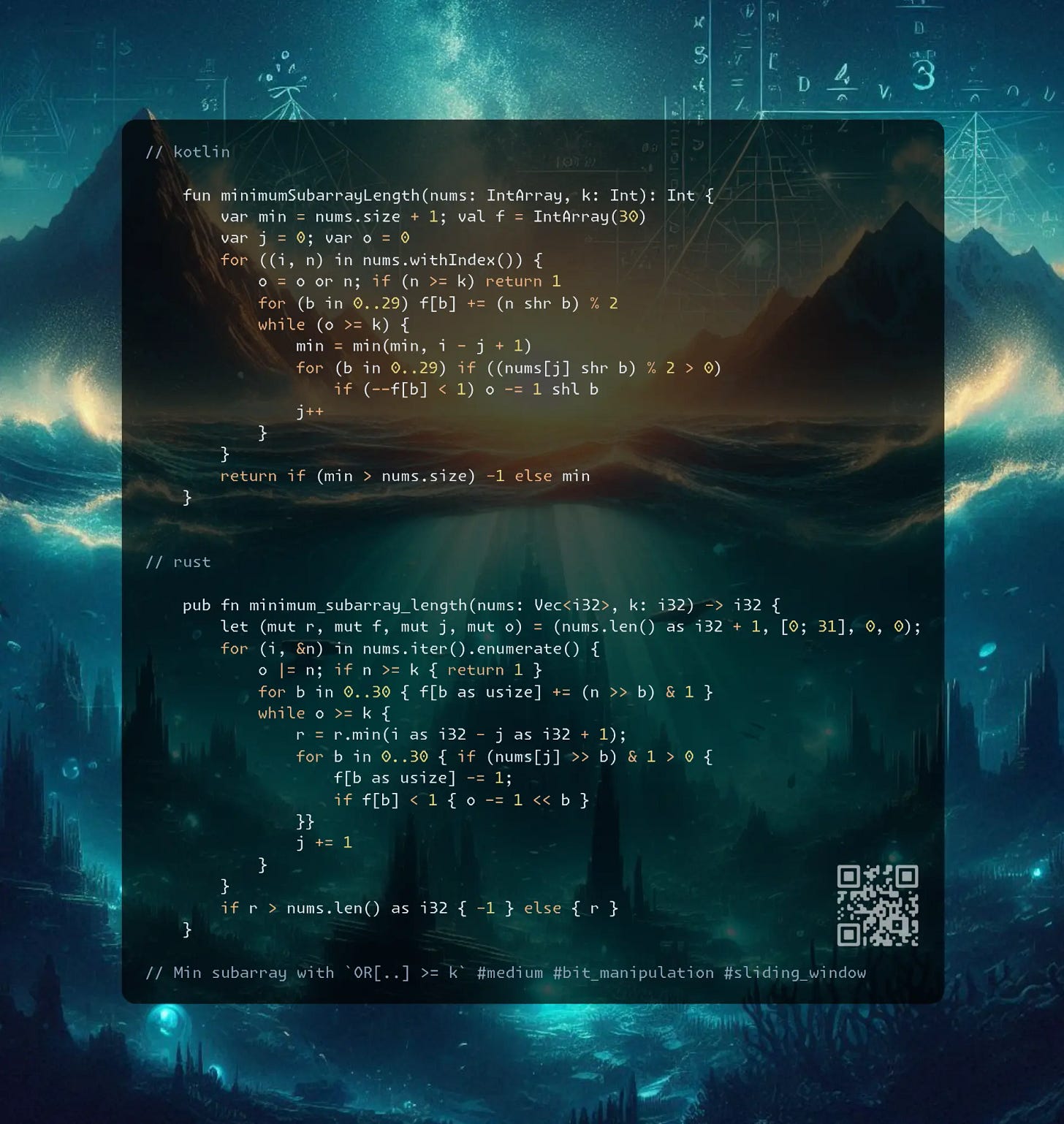
Min subarray with OR[..] >= k #medium #bit_manipulation #sliding_window
Intuition
First, don't solve the wrong problem, OR[..] must be at least k, not the exact k.
Now, the simple idea is to use the Sliding Window technique: expand it with each number, calculating the OR. However, the shrinking is not trivial, as the OR operation is not reversable. So, we should track how each number bits are add in the final OR result to be able to remove them. To do this, count each bit frequency.
Another way to look at this problem is no maintain the most recent index of each bit:
// not exact, but 'at least k'!
// k=101
// 1000 <-- good, bigger than b101, any number with higher bit => 1
// 110 <-- good, bigger than b101, any number with same prefix => 1
// 010 <---------------------------.
// 001 -> search for second bit |
// *011 -> update pos for first bit | this OR will give 110 > 101, good
// 000 |
// *100 <-- second bit--------------J
This solution is more complex, as we should analyze every bit for possible corner cases.
Approach
one optimization is if the number is bigger than k we can return 1
pointers approach is a single-pass but is slower than frequencies approach for the test dataset (30ms vs 5ms)
Complexity
Time complexity: $$O(n)$$
Space complexity: $$O(n)$$
Code
fun minimumSubarrayLength(nums: IntArray, k: Int): Int {
var min = nums.size + 1
val pos = IntArray(32) { -1 }
for ((i, n) in nums.withIndex()) {
if (n >= k) return 1
var max = -1; var all = true
for (b in 31 downTo 0) {
if ((n shr b) % 2 > 0) pos[b] = i
val kBit = (k shr b) % 2 > 0
if (kBit && pos[b] < 0) all = false
if (all && !kBit && pos[b] >= 0) min = min(min, max(max, i - pos[b] + 1))
if (all && kBit) max = max(max, i - pos[b] + 1)
}
if (all) min = min(min, max)
}
return if (min > nums.size) -1 else min
}
fun minimumSubarrayLength(nums: IntArray, k: Int): Int {
var min = nums.size + 1; val f = IntArray(30)
var j = 0; var o = 0
for ((i, n) in nums.withIndex()) {
o = o or n; if (n >= k) return 1
for (b in 0..29) f[b] += (n shr b) % 2
while (o >= k) {
min = min(min, i - j + 1)
for (b in 0..29) if ((nums[j] shr b) % 2 > 0)
if (--f[b] < 1) o -= 1 shl b
j++
}
}
return if (min > nums.size) -1 else min
}
pub fn minimum_subarray_length(nums: Vec<i32>, k: i32) -> i32 {
let (mut r, mut f, mut j, mut o) = (nums.len() as i32 + 1, [0; 31], 0, 0);
for (i, &n) in nums.iter().enumerate() {
o |= n; if n >= k { return 1 }
for b in 0..30 { f[b as usize] += (n >> b) & 1 }
while o >= k {
r = r.min(i as i32 - j as i32 + 1);
for b in 0..30 { if (nums[j] >> b) & 1 > 0 {
f[b as usize] -= 1;
if f[b] < 1 { o -= 1 << b }
}}
j += 1
}
}
if r > nums.len() as i32 { -1 } else { r }
}
int minimumSubarrayLength(vector<int>& a, int k) {
int r = a.size() + 1, j = 0, o = 0, b = 0;
int f[31] = {};
for (int i = 0; i < a.size(); ++i) {
if (a[i] >= k) return 1;
for (b = 0; b < 30; b++) f[b] += a[i] >> b & 1;
for (o |= a[i]; o >= k; j++)
for (r = min(r, i - j + 1), b = 0; b < 30; b++)
if ((a[j] >> b & 1) && !--f[b]) o -= 1 << b;
}
return r > a.size() ? -1 : r;
}
Thanks for reading DMITRII’s Substack! Subscribe for free to receive new posts and support my work.
