This is a choice problem: either pick or skip. The trick is to define cacheable subproblem, otherwise it is 2^n time complexity.
One accepted way is to cache possible unique subset sums from the suffix array. (slow, but accepted, O(ns), where s is a unique sums count).
Another way, is to set target and search for any subset that has this sum. O(ns).
Bottom-up is the fastest: for the current value, mark down starting from the target - x.
Approach
The clever optimization is a bitset: each bit is a subset sum, we can mark all at once by shifting entire set by x
Complexity
Time complexity: $$O(ns)$$, s is up to max * (max + 1) / 2 for unique seq 1,2,3...max, so it is O(nm^2)
Space complexity: $$O(n)$$
Code
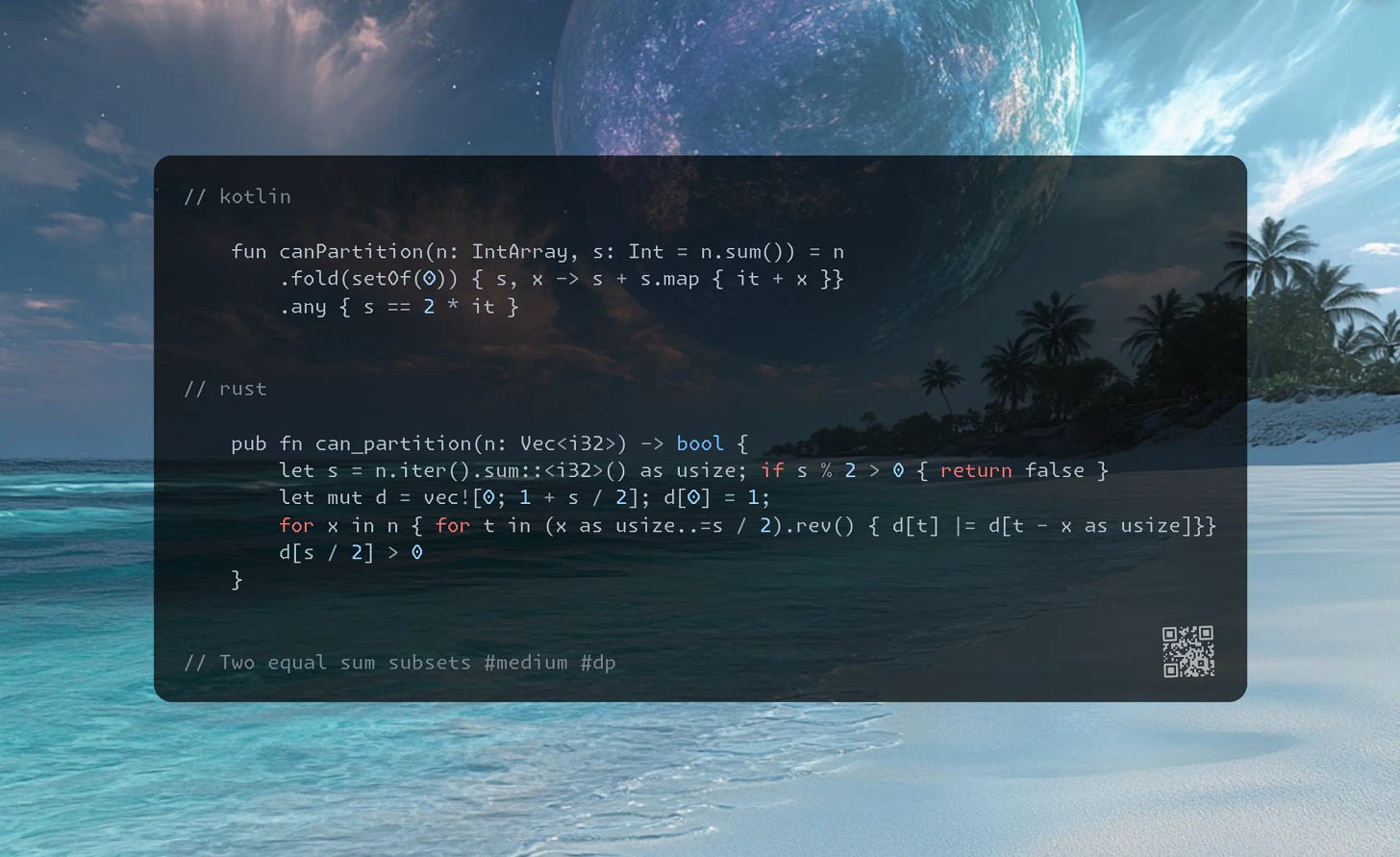
fun canPartition(n: IntArray, s: Int = n.sum()) = n
.fold(setOf(0)) { s, x -> s + s.map { it + x }}
.any { s == 2 * it }
fun canPartition(nums: IntArray): Boolean {
val sum = nums.sum(); var sums = setOf(0)
for (x in nums) sums += sums.map { it + x }
return sums.any { sum - it == it }
}
fun canPartition(nums: IntArray): Boolean {
val sum = nums.sum(); val dp = HashMap<Int, Set<Int>>()
fun dfs(i: Int): Set<Int> = if (i == nums.size) setOf(0) else
dp.getOrPut(i) {
dfs(i + 1) + dfs(i + 1).map { it + nums[i] }
}
return dfs(0).any { sum - it == it }
}
fun canPartition(n: IntArray): Boolean {
n.sort()
val sum = n.sum(); if (sum % 2 > 0) return false
val dp = HashMap<Pair<Int, Int>, Boolean>()
fun dfs(i: Int, t: Int): Boolean = if (i == n.size) t == 0 else
t >= 0 && dp.getOrPut(i to t) {
dfs(i + 1, t - n[i]) || dfs(i + 1, t)
}
return dfs(0, sum / 2)
}
fun canPartition(n: IntArray): Boolean {
val s = n.sum(); if (s % 2 > 0) return false
val d = IntArray(s / 2 + 1); d[0] = 1
for (x in n) for (t in s / 2 downTo x) d[t] += d[t - x]
return d[s / 2] != 0
}
pub fn can_partition(n: Vec<i32>) -> bool {
let s = n.iter().sum::<i32>() as usize; if s % 2 > 0 { return false }
let mut d = vec![0; 1 + s / 2]; d[0] = 1;
for x in n { for t in (x as usize..=s / 2).rev() { d[t] |= d[t - x as usize]}}
d[s / 2] > 0
}
bool canPartition(vector<int>& n) {
int s = 0; bitset<10001> b(1);
for (int x: n) s += x, b |= b << x;
return (1 - s & 1) * b[s / 2];
}
Thanks for reading DMITRII’s Substack! This post is public so feel free to share it.
