# 05.08.2023 [95. Unique Binary Search Trees II]

All possible Binary Search Trees for 1..n numbers

05.08.2023

95. Unique Binary Search Trees II medium
blog post

Join me on Telegram

https://t.me/leetcode_daily_unstoppable/299

Problem TLDR

All possible Binary Search Trees for 1…n numbers

Intuition

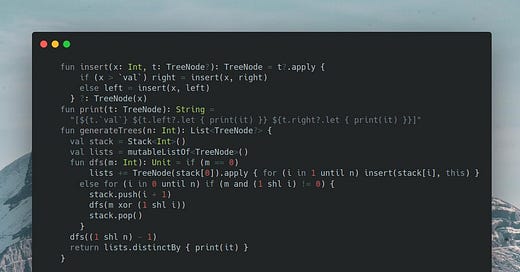
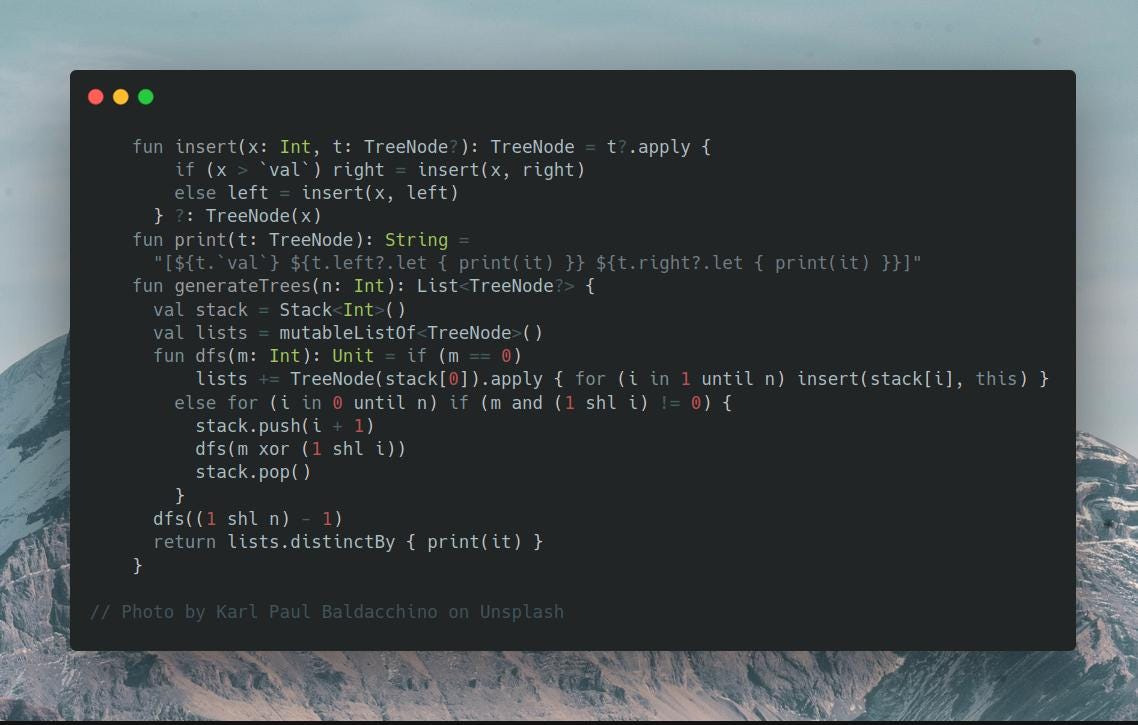
One way to build all possible BST is to insert numbers in all possible ways. We can do this with a simple backtracking, given the small n <= 8. To remove duplicates, we can print the tree and use it as a hash key.

Approach

• use a bit mask and a Stack for backtracking

Complexity

• Time complexity:

O(n!∗nlog(n)), as the recursion depth is n, each time iterations go as n * (n - 1) * (n - 2) * … * 2 * 1, which is equal to n!. The final step of inserting elements is nlog(n), and building a hash is n, which is < nlogn, so not relevant.

• Space complexity:

O(n!), is a number of permutations

Code

    fun insert(x: Int, t: TreeNode?): TreeNode = t?.apply {
        if (x > `val`) right = insert(x, right)
        else left = insert(x, left)
      } ?: TreeNode(x)
    fun print(t: TreeNode): String = 
      "[${t.`val`} ${t.left?.let { print(it) }} ${t.right?.let { print(it) }}]"
    fun generateTrees(n: Int): List<TreeNode?> {
      val stack = Stack<Int>()
      val lists = mutableListOf<TreeNode>()
      fun dfs(m: Int): Unit = if (m == 0) 
          lists += TreeNode(stack[0]).apply { for (i in 1 until n) insert(stack[i], this) }
        else for (i in 0 until n) if (m and (1 shl i) != 0) {
          stack.push(i + 1)
          dfs(m xor (1 shl i))
          stack.pop()
        }
      dfs((1 shl n) - 1)
      return lists.distinctBy { print(it) }
    }

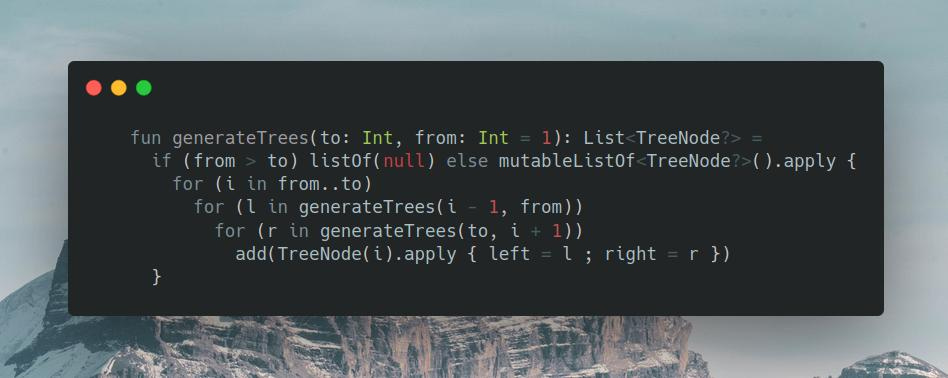
Another divide-and-conquer solution, that I didn't think of